Gaussian beam
The fundamental Gaussian beam
`E(r,z)=E_0 omega_0/{omega(z)} exp(-r^2/{omega(z)^2})exp(-ikz-ik r^2/{2 R(z)}+i k zeta(z))`
wave length
beam waist
amplitude
z-axis
r-axis
frequency f
`c=lambda f`
wave number k
`k={2pi}/lambda`
waist to wave length ratio
\(\frac{\omega}{\lambda}\)
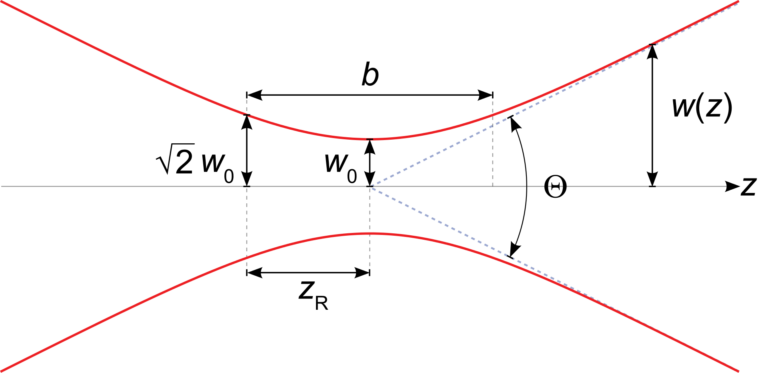
Rayleigh range \(z_R\)
`z_R=1/2 omega_0^2 k`
beam width `omega(z)`
`omega(z)=omega_0 sqrt(1+(z/z_R)^2)`
wavefront curvature R(z)
`R(z)=z[1+(z_R/z)^2]`
Gouy phase `phi(z)`
`phi(z)=arctan(z/z_R)`
Beam divergency `theta`
`theta=lim_{z rarr oo}{omega(z)}/z=arctan(2/{omega_0 k})`
Max Intensity `I_0`
`I_0=|E_0|^2/{2 eta}`
Total power `P_0`
`P_0=1/2 I_0 pi omega_0^2`
Itensity `I(r,z)`
`I(r,z)=I_0(omega_0/{omega(z)})^2 exp({-2r^2}/{omega(z)^2})`
power ratio p(r,z)
`p(r,z)=1-exp({-2r^2}/{omega(z)^2})`
Beam quality BPP
`BPP=theta*omega_0`
`|E(r,z)|`
`E_0 omega_0/{omega(z)} exp(-r^2/{omega(z)^2})`
`Arg(E)`
`k z+k r^2/(2R(z))-phi(z)`
Arg
Arg in degree
Electric field E(r,z)
`E(r,z)=E_0 omega_0/{omega(z)} exp(-r^2/{omega(z)^2})exp(-ikz-ik r^2/{2 R(z)}+i zeta(z))`
replace string
beam parameter `q(z)`
`q(z)=z+iz_R`
reciprocal of q(z) `1/(q(z))`
`1/q(z)=1/(R(z))-i lambda/(n pi omega^2(z))`
Electric Field `E(r,z)`
`E(r,z)=1/(q(z))exp(-jk r^2/(2q(z)))`